Comprimento da circunferência
Quando somamos todos os lados de uma figura plana iremos obter o seu perímetro, no caso específico do círculo, o cálculo do seu perímetro é dado pelo comprimento da circunferência (contorno do círculo), pois um círculo é contornado por uma circunferência
é contornado por uma circunferência que é formada pela união das extremidades de uma linha aberta
que é formada pela união das extremidades de uma linha aberta .
.
c = constante
2r
c = π
2r
c = 2 π r
Exemplo 1
Vamos calcular o comprimento de uma circunferência de 7 cm de raio, considerandoπ = 3,14. C= 2 π r
C= 2 x 3,14 x 7
C= 43,96 cm
Disponível em: http://mundoeducacao.uol.com.br/matematica/comprimento-circunferencia.htm
Comprimento de um Arco
Dada uma circunferência de centro O, raio r e dois pontos A e B pertencentes à circunferência, temos que a distância entre os pontos assinalados é um arco de circunferência. O comprimento de um arco é proporcional à medida do ângulo central, quanto maior o ângulo, maior o comprimento do arco; e quanto menor o ângulo, menor o comprimento do arco.
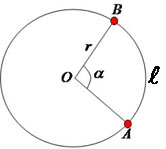
Para determinarmos o comprimento de uma circunferência utilizamos a seguinte expressão matemática: C = 2*π*r. A volta completa em uma circunferência é representada por 360º. Vamos realizar uma comparação entre o comprimento da circunferência em medida linear (ℓ) e medida angular (α), observe:
linear | angular |
2*π*r | 360º |
ℓ | α |
circunferência de raio r e ângulo central α
em graus. Nesses casos utilize π = 3,14.
Caso o ângulo central seja dado em radiano
utilizamos a seguinte expressão: ℓ = α * r.
ℓ = α * π * r
180º ℓ = 30º * 3,14 * 2 O comprimento do arco será de 1,05 centímetros.
180º ℓ = 188,40
180 ℓ = 1,05 cm
AREA DO SETOR CIRCULAR
 A área total de um círculo é proporcional ao tamanho do raio e pode ser calculada pela expressão π * r², na qual π equivale a 3,14 e r é a medida do raio do círculo. O círculo pode ser dividido em infinitas partes, as quais recebem o nome de arcos (partes de um círculo). Os arcos de uma região circular são determinados de acordo com a medida do ângulo central, e é com base nessa informação que calcularemos a área de um segmento circular.
A área total de um círculo é proporcional ao tamanho do raio e pode ser calculada pela expressão π * r², na qual π equivale a 3,14 e r é a medida do raio do círculo. O círculo pode ser dividido em infinitas partes, as quais recebem o nome de arcos (partes de um círculo). Os arcos de uma região circular são determinados de acordo com a medida do ângulo central, e é com base nessa informação que calcularemos a área de um segmento circular. Uma volta completa no círculo corresponde a 360º, valor que podemos associar à expressão do cálculo da área do círculo, π * r². Partindo dessa associação podemos determinar a área de qualquer arco com a medida do raio e do ângulo central, através de uma simples regra de três. Observe:
360º ------------- π * r²
θº ------------------ x
onde: π = 3,14
r = raio do círculo
θº = medida do ângulo central
x = área do arco
Exemplo 1: Determine a área de um segmento circular com ângulo central de 32º e raio medindo 2 m.
Resolução:
360º ------------- π * r² 360x = 32 * π * r²
32º ------------------ x x = 32 * π * r²
360
x = 32 * 3,14 * 2²
360
x = 32 * 3,14 * 4
360
x = 401,92
360
x = 1,12
DISPOONÍVEL EM: http://mundoeducacao.uol.com.br/matematica/area-
Área da Coroa do Círculo
Quando duas ou mais circunferências possuem o mesmo centro, são denominadas concêntricas. Nesse caso elas podem ter raio de tamanhos diferentes. Observe:
Ao unirmos duas circunferências de mesmo centro com raios R e r, considerando R > r, temos que a diferença entre as áreas é denominada coroa circular. Observe:

A área da coroa circular representada pode ser calculada através da diferença entre as áreas totais das duas circunferências, isto é, área do círculo maior menos a área do círculo menor.
Área da coroa = Área do círculo maior – Área do círculo menor
Área da coroa = (π * R²) – (π * r²)
Área da coroa = π * (R² – r²)
Observação: Os resultados podem ser dados em função de π, caso seja necessário substitua π por seu valor aproximado, 3,14.
Exemplo 1 :Determine a área da coroa circular da figura a seguir, considerando o raio da circunferência maior igual a 10 metros e raio da circunferência menor igual a 8 metros.
Resolução:
A = π * (R² – r²)
A = π * (10² – 8²)
A = π * (100 – 64)
A = π * 36
A = 36π m² ou A = 36 * 3,14
A = 113,04 m²

Exemplo 2:
Um cavalo está amarrado em uma árvore através de uma corda de 20 metros de comprimento. A área total da pastagem possui raio de 50 metros de comprimento. Considerando a área de pastagem máxima do cavalo, determine a área não utilizada na alimentação do cavalo.
Resolução:

A = π * (50² – 20²)
A = π * (2500 – 400)
A = π * (2100)
A = π * 2100
A = 2100π m² ou A = 2100 * 3,14
A = 6594 cm²
Disponível em: http://mundoeducacao.uol.com.br/matematica/area-coroa-circulo.htm
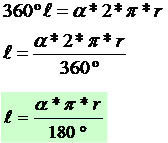
2 comentários:
está muito bom e bem explicado e não está muito grande e da para comprieender muito bem sobre Comprimento da circunferência.
Quando eu faço as coisas, eu coloco para quebrar. Obrigado pelos elogios.
Postar um comentário