Posições entre Retas e Circunferência
Reta externa à circunferência
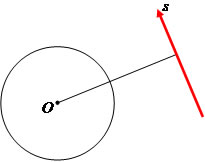
A reta s é externa à circunferência de centro O e raio R, então podemos propor a seguinte situação: a distância do centro da circunferência à reta s é maior que o raio da circunferência.
D > R
A reta s é externa à circunferência de centro O e raio R, então podemos propor a seguinte situação: a distância do centro da circunferência à reta s é maior que o raio da circunferência.
D > R
Reta tangente à circunferência
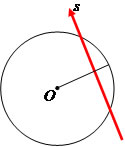
A reta s é tangente à circunferência de centro O e raio R, isto é, a reta s possui um ponto em comum com a circunferência, por isso podemos dizer que a distância entre centro O até a reta s possui a mesma medida.
D = R
Reta secante à circunferência
A reta s é secante à circunferência de raio R e centro O, a reta intersecta a circunferência em dois pontos. Nesse caso constatamos que a medida do raio da circunferência é maior que a medida da reta secante.
D < R
A reta s é tangente à circunferência de centro O e raio R, isto é, a reta s possui um ponto em comum com a circunferência, por isso podemos dizer que a distância entre centro O até a reta s possui a mesma medida.
D = R
Reta secante à circunferência
A reta s é secante à circunferência de raio R e centro O, a reta intersecta a circunferência em dois pontos. Nesse caso constatamos que a medida do raio da circunferência é maior que a medida da reta secante.
D < R
Posições relativas entre duas circunferências
Não possuem pontos em comum
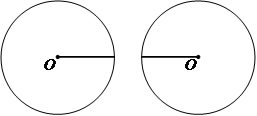
Externas
D > r1 + r2
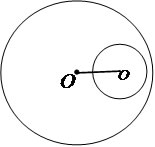
Internas
D < r1 – r2
Possuem um ponto em comum
Tangentes: as circunferências possuem um ponto em comum.
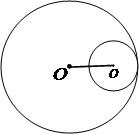
Tangentes internas
D = r1 – r2
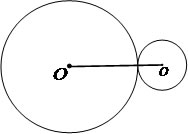
Tangentes externas
D = r1 + r2
D = r1 + r2
Possuem dois pontos em comum
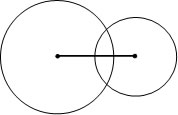
Secante: possuem dois pontos em comum.
r1 – r2 < D < r1 + r2
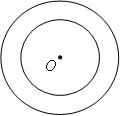
Circunferências concêntricas
São circunferências que possuem o mesmo centro, não existindo distância entre eles.
D = 0
Relação entre Secante e Tangente
Cossecante
Por definição, cossecante é a relação do inverso do seno.
Assim: cossecX = 1/senX
Dado um número real x , tal que x
kπ, considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do seno no ponto C, definimos por cossecante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto C.
Quando o ângulo é do primeiro ou do segundo quadrante seu sinal é positivo, quando do terceiro ou quarto seu sinal é negativo.
Por definição temos que secante é a relação do inverso do cosseno.
Assim: secX = 1/cosX
Dado um número real x , tal que x ã/2 + kã , considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do cosseno no ponto C, definimos por secante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto S.
Quando o ângulo é do primeiro ou do quarto quadrante seu sinal é positivo, quando do segundo ou do terceiro seu sinal é negativo.
Por definição temos que cotangente é a relação do inverso da tangente.
Assim: cotgX = 1/tanX = cosX / senX
Dado um número real x , tal que x kã, considerando a reta d tangente ao circulo trigonométrico no ponto B seja D o ponto de intersecção da reta d com o segmento OP, definimos por cotangente o módulo do segmento que vai do ponto B até o ponto D.
Sinal da cotangente
Quando o ângulo é do primeiro ou do terceiro quadrante seu sinal é positivo, quando do segundo ou do quarto seu sinal é negativo.
COMPONENTES: JEAN SOUZA
RAFAEL BRITO
TAINA RIOS
Por definição, cossecante é a relação do inverso do seno.
Assim: cossecX = 1/senX
Dado um número real x , tal que x
kπ, considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do seno no ponto C, definimos por cossecante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto C.Quando o ângulo é do primeiro ou do segundo quadrante seu sinal é positivo, quando do terceiro ou quarto seu sinal é negativo.
Por definição temos que secante é a relação do inverso do cosseno.
Assim: secX = 1/cosX
Dado um número real x , tal que x
ã/2 + kã , considerando a reta s tangente ao circulo trigonométrico no ponto P que intercepta o eixo do cosseno no ponto C, definimos por secante o módulo do segmento que vai do centro da circunferência trigonométrica até o ponto S.Quando o ângulo é do primeiro ou do quarto quadrante seu sinal é positivo, quando do segundo ou do terceiro seu sinal é negativo.
Por definição temos que cotangente é a relação do inverso da tangente.
Assim: cotgX = 1/tanX = cosX / senX
Dado um número real x , tal que x
kã, considerando a reta d tangente ao circulo trigonométrico no ponto B seja D o ponto de intersecção da reta d com o segmento OP, definimos por cotangente o módulo do segmento que vai do ponto B até o ponto D.Sinal da cotangente
Quando o ângulo é do primeiro ou do terceiro quadrante seu sinal é positivo, quando do segundo ou do quarto seu sinal é negativo.
COMPONENTES: JEAN SOUZA
RAFAEL BRITO
TAINA RIOS
PAULO DE TARSO
LUDMILA XAVIER
Um comentário:
ficou muito bom esse grupo...o texto está de fácil entendimento para os leitores e fala um pouco sobre as posições das retas na circunferência deu para aprender bastante
Postar um comentário